|
Подписка на рассылку
ОТЗЫВЫ КЛИЕНТОВ
Сегодня получила платье от Виктории Бекхам. Размер подошёл, но длину чуть-чуть укорочу, т.к. люблю по-короче. Качество отличное. Доставка тоже порадовала, пришло уведомление на 7 день, получила утром на 8 день. Куда хотела в нём пойти - пойду, всё успели, не ожидала, что так быстро получится. Очень сомневалась, но зря. Спасибо!!!
|
Выкройка овального и наклонного конуса. Объемный конусКонус как геометрическая фигураКонус (с греческого «konos») – сосновая шишка. Конус знаком людям с глубокой древности. В 1906 году была обнаружена книга «О методе», написанная Архимедом (287-212 гг. до н. э.), в этой книге дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед говорит, что это открытие принадлежит древнегреческому философу Демокриту (470-380 гг. до н.э.), который с помощью данного принципа получил формулы для вычисления объема пирамиды и конуса. Конус (круговой конус) – тело, которое состоит из круга – основание конуса, точки, не принадлежащей плоскости этого круга, – вершины конуса и всех отрезков, соединяющих вершину конуса и точки окружности основания. Отрезки, которые соединяют вершину конуса с точками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности. Конус называется прямым, если прямая, которая соединяет вершину конуса с центром основания, перпендикулярна плоскости основания. Прямой круговой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого конуса называется прямая, содержащая его высоту. Сечение конуса плоскостью, проходящей через образующую конуса и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью конуса. Плоскость, перпендикулярная оси конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса. Плоскость, перпендикулярная оси конуса отсекает от него меньший конус. Оставшаяся часть называется усечённым конусом. Объём конуса равен трети произведения высоты на площадь основания. Таким образом, все конусы, опирающиеся на данное основание и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны. Площадь боковой поверхности конуса можно найти по формуле: Sбок = πRl, где R – радиус основания, l – длина образующей. Площадь полной поверхности конуса находится по формуле: Sкон = πRl + πR2, где R – радиус основания, l – длина образующей. Объём кругового конуса равен V = 1/3 πR2H, где R – радиус основания, Н – высота конуса Площадь боковой поверхности усеченного конуса можно найти по формуле: Sбок = π(R + r)l, где R – радиус нижнего основания, r – радиус верхнего основания, l – длина образующей. Площадь полной поверхности усеченного конуса можно найти по формуле: Sкон = πR2 + πr2 + π(R + r)l, где R – радиус нижнего основания, r – радиус верхнего основания, l – длина образующей. Объём усечённого конуса можно найти следующим образом: V = 1/3 πH(R2 + Rr + r2), где R – радиус нижнего основания, r – радиус верхнего основания, Н – высота конуса. © blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна. blog.tutoronline.ru Цилиндр, конус, шар, развёртка цилиндра и конусаЦилиндр, конус и шар относятся к объемным (трехмерным) геометрическим фигурам вращения. Объемные фигуры вращения (еще говорят — «тела», подразумевая объемность фигуры), как правило, образованы вращением плоской фигуры вокруг какой-то линии (прямой). Так, цилиндр — это фигура, полученная от вращения прямоугольника вокруг одной из его сторон как оси; конус — вращением прямоугольного треугольника вокруг его катета как оси, шар — вращением полукруга вокруг его диаметра как оси. Объемные фигуры бывают прямые (прямой цилиндр, прямой конус) и наклонные (наклонный цилиндр, наклонный конус), что зависит от вида той плоской геометрической фигуры, которая их образует. В курсе математики для б класса рассматриваются только прямые цилиндры и конусы . Определение. Цилиндр — это тело (объемная геометрическая фигура), полученное вращением прямоугольника вокруг одной из его сторон как оси.
Определение. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.
Определение. Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси.
Развертки цилиндра и конусаРазверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры. Развертка цилиндра приведена схематически. Развертка конуса приведена схематически. Площади боковой поверхности цилиндра и конусаПравило. Площадь боковой поверхности цилиндра равна произведению длины окружности основания и высоты цилиндра. где C — длина окружности, H — высота цилиндра, R — радиус окружности основания. Правило. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса. где C — длина окружности основания, l — длина образующей конуса, R — радиус основания. Площадь поверхности шараПравило. Площадь поверхности шара равна учетверенной площади большого круга шара. где R — радиус шара. Объемы цилиндра, конуса и шараПравило. Объем цилиндра равен произведению площади основания н высоты. где R — радиус основания, H — высота цилиндра. Правило. Объем конуса равен одной трети произведения площади основания и высоты конуса. где R — радиус основания, H — высота конуса. Правило. Объем шара равен четырем третямпроизведения числа Пи на куб радиуса.
где R — радиус шара. shkolo.ru Формулы объема, площади поверхности, объем конуса, объем цилиндра, объем шара
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло. Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
Ты нашел то, что искал? Поделись с друзьями! Смотрите также: Формулы объема и площади поверхности многогранников.Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты. Например, такой важный факт: Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем - в 8 раз. (ведь , ). Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ. 1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур. Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу. 2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду? Говорят, что хороший чертеж - это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии. Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ». А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней. Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве) Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним. ege-study.ru
gavrilovart.ru Конус [wiki.eduVdom.com]Конусом (прямым круговым конусом) называется тело, состоящее из круга (основания конуса), точки, не лежащей в плоскости этого круга (вершины конуса), и всех отрезков, соединяющих вершину конуса с точками основания. Конус является телом вращения. Конус Рис.1 Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Конус — тело, которое ограничено конической поверхностью и плоскостью, на которой лежат концы образующих конической поверхности. Коническая поверхность — поверхность, которая образуется движением отрезка, один из концов которого неподвижен, а другой перемещается на плоскости вдоль некоторой кривой. Отрезки называют образующими конической поверхности, а кривую – направляющей. Неподвижная точка – вершина конической поверхности. Боковая поверхность конуса — часть конической поверхности, ограниченная плоскостью. Основание конуса — часть плоскости, отсекаемая боковой поверхностью конуса. Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания (См.Рис.1). В противном случае, конус называется наклонным. В школьном курсе изучается прямой круговой конус. Круговой конус — конус, у которого в основании круг. Прямой круговой конус (просто конус) — круговой конус, у которого прямая, соединяющая вершину конуса с центром круга, лежащего в основании, перпендикулярна плоскости основания. Ось конуса — прямая, проходящая через вершину конуса и центр основания конуса. Высота конуса — отрезок оси конуса, соединяющий вершину конуса с центром основания. Конус можно рассматривать как тело, полученное вращением прямоугольного треугольника вокруг прямой, содержащей его катет. Образующие конуса совпадают с образующими конической поверхности. Сечение конуса плоскостью, проходящей через его ось, называется осевым сечением. Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проведенному через эту образующую, называется касательной плоскостью конуса. См.Рис.2. Рис.2 Развёртка боковой поверхности конуса — круговой сектор, радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса. Площадь боковой поверхности (круглого) конуса равна произведению половины длины окружности основания (C) на образующую (l): $$S_{бок}=\frac{1}{2}\cdot Cl=\pi\cdot rl$$ , где r – радиус основания, l – длина образующей. Площадь полной поверхности конуса — сумма площадей основания конуса и его боковой поверхности, которая записывается формулой: $$S_{полн}=\pi\cdot r(l+r)$$ , где r — радиус основания, l — длина образующей. Объем всякого конуса равен трети произведения площади основания (S) на высоту (h): $$V=\frac{1}{3}\cdot Sh$$ Объем круглого конуса: $$V=\frac{1}{3}\cdot Sh=\frac{1}{3}\cdot\pi r^2 \cdot h$$ Усеченный конус – это часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания. См.Рис.3. Усечённый конус Рис.3 Формулы для усечённого конуса (См.Рис.4): $$ S_{бок}=\pi\cdot l\cdot (R+r) \\ S_{полн}=S_{бок}+\pi(R^2+r^2) \\ V=\frac{1}{3}\pi\cdot h(R^2+R\cdot r+r^2) $$ Усечённый конус Рис.4 Пример 1. Высота конуса равна 4 , а длина образующей - 5. Найдите диаметр основания конуса. Видео-решение. wiki.eduvdom.com Элементы конуса — урок. Геометрия, 11 класс.Осевое сечение конуса — это равнобедренный треугольник.\(APB\) — осевое сечение конуса. ∡PAO=∡PBO — углы между образующими и основанием конуса. Развёрткой боковой поверхности конуса является круговой сектор. Длина дуги сектора — это длина окружности основания конуса длиной 2πR, угол развёртки боковой поверхности α. В конусе нельзя обозначить угол развёртки.На развёртке конуса нельзя обозначить высоту и радиус конуса.

Радиус сектора — это образующая конуса.

Таким образом, боковая поверхность конуса является частью полного круга с радиусом \(l\): Sбок.=πl2⋅α360°
Длина дуги также является частью длины полной окружности с радиусом \(l\), но в то же время длина дуги — это длина окружности основания конуса с радиусом \(R\). Сравним выражения длины дуги и выразим α через \(R\):
2πl⋅α360°=2πRα=2πR⋅360°2πl=R⋅360°l
Получаем ещё одну формулу боковой поверхности конуса, не используется угол развёртки боковой поверхности:
Sбок.=πl2⋅R⋅360°360°⋅l=πRl Усечённый конус Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых — конус, а другую часть называют усечённым конусом. 
Также усечённый конус можно рассматривать как тело вращения, которое образовалось в результате вращения прямоугольной трапеции вокруг боковой стороны (которая перпендикулярна к основанию трапеции) или в результате вращения равнобедренной трапеции вокруг высоты, проведённой через серединные точки оснований трапеции.

OO1 — ось конуса и высота конуса. AA1 — образующая конуса. Круги с центрами \(O\) и O1 — основания усечённого конуса. \(AO\) и A1O1 — радиусы оснований конуса. Осевое сечение конуса — это сечение конуса плоскостью, которая проходит через ось OO1 конуса. Осевое сечение конуса — это равнобедренная трапеция.AA1B1B — осевое сечение конуса.
Боковая поверхность определяется как разность боковой поверхности данного конуса и отсечённого конуса:
Sбок.=πR⋅PA−πr⋅PA1=πR⋅PA1+AA1−πr⋅PA1==πR⋅PA1+πR⋅AA1−πr⋅PA1==πR⋅l+πR−πr⋅PA1
Так как ΔPAO∼ΔPA1O1, то стороны их пропорциональны:
PAPA1=Rrl+PA1PA1=Rrr⋅l+PA1=R⋅PA1rl=R⋅PA1−r⋅PA1PA1⋅R−r=rlPA1=rlR−r
Таким образом получаем формулу боковой поверхности усечённого конуса, которая содержит радиусы оснований и образующую усечённого конуса:
Sбок.=πRl+π⋅PA1⋅R−r=πRl+π⋅rlR−r⋅R−rSбок.=πRl+πrl=πl⋅R+r www.yaklass.ru Выкройка овального и наклонного конуса24.09.2014 // Владимир Трунов
Теперь речь пойдет о том, как построить выкройку (развертку) для овального и наклонного конуса. Под овальным конусом будем подразумевать конус, в основании которого лежит эллипс (как наиболее гармоничный из овалов). Наклонным конусом назовем конус, проекция вершины которого (или мнимой вершины, если конус усеченный) на плоскость основания не совпадает с центром эллипса.И тут я должен сообщить две новости, как водится, хорошую и плохую. Начну с плохой. Не существует простых формул для построения таких выкроек. Есть только жуткие интегралы. Но в них мы закапываться не будем благодаря хорошей новости: у нас есть компьютер. И есть такое понятие как численные методы. Коротко говоря, это выполнение огромного количества простейших операций над числами, в результате которых появляется возможность решить задачу, нерешаемую аналитически (то есть при помощи формул). И надо только найти человека, который изобрел бы алгоритм для решения нашей задачи, и хорошо ему заплатить. К счастью, такой человек нашелся, придумал алгоритм, запрограммировал его и публикует сегодня в виде новой версии программы Cones. Зовут его Владимир Трунов, и все благодарности — к нему. Нет никакого смысла вникать в подробности численного метода, реализованного в программе Cones для построения выкроек овальных и наклонных конусов. Скажу только, что основой его является разбиение эллипса на множество мелких отрезков и вычисление для каждой вершины полученного многоугольника значений длины образующей конуса и приращения угла развертки. Благодаря этому в вычислениях используются только тригонометрические функции и теорема Пифагора. Понятно, что полученные значения, а стало быть и рисунок, построенный по ним, имеют некоторую погрешность. Эта погрешность тем меньше, чем ближе конус к круглому и прямому. Если отношение большего диаметра эллипса к меньшему не превышает 2, а угол наклона оси (от вертикали) — не более 30 градусов, то погрешность в линейных размерах боковой поверхности выкройки не выйдет за 1%. (В более экзотических случаях погрешность может быть и больше, но в следующих версиях программы алгоритм будет совершенствоваться с целью ее минимизации.) tvlad.ru |

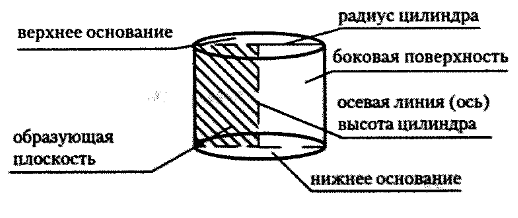
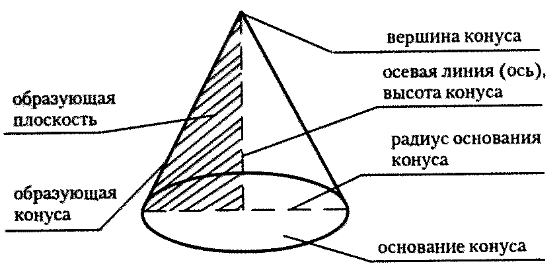


 Тела вращения, изучаемые в школе, - это цилиндр, конус и шар.
Тела вращения, изучаемые в школе, - это цилиндр, конус и шар.
 Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.
Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум. Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в 














 В статье Выкройка для конуса мы рассмотрели построение выкройки для круглого прямого конуса, то есть конуса, имеющего в основании круг, и ось которого перпендикулярна основанию. Там мы обошлись несколькими простыми формулами.
В статье Выкройка для конуса мы рассмотрели построение выкройки для круглого прямого конуса, то есть конуса, имеющего в основании круг, и ось которого перпендикулярна основанию. Там мы обошлись несколькими простыми формулами.









