|
Подписка на рассылку
ОТЗЫВЫ КЛИЕНТОВ
Сегодня получила платье от Виктории Бекхам. Размер подошёл, но длину чуть-чуть укорочу, т.к. люблю по-короче. Качество отличное. Доставка тоже порадовала, пришло уведомление на 7 день, получила утром на 8 день. Куда хотела в нём пойти - пойду, всё успели, не ожидала, что так быстро получится. Очень сомневалась, но зря. Спасибо!!!
|
Формулы объема и площади поверхности. Цилиндр, конус и шар. Конус объемныйЦилиндр, конус, шар, развёртка цилиндра и конусаЦилиндр, конус и шар относятся к объемным (трехмерным) геометрическим фигурам вращения. Объемные фигуры вращения (еще говорят — «тела», подразумевая объемность фигуры), как правило, образованы вращением плоской фигуры вокруг какой-то линии (прямой). Так, цилиндр — это фигура, полученная от вращения прямоугольника вокруг одной из его сторон как оси; конус — вращением прямоугольного треугольника вокруг его катета как оси, шар — вращением полукруга вокруг его диаметра как оси. Объемные фигуры бывают прямые (прямой цилиндр, прямой конус) и наклонные (наклонный цилиндр, наклонный конус), что зависит от вида той плоской геометрической фигуры, которая их образует. В курсе математики для б класса рассматриваются только прямые цилиндры и конусы . Определение. Цилиндр — это тело (объемная геометрическая фигура), полученное вращением прямоугольника вокруг одной из его сторон как оси.
Определение. Конус (прямой) — это тело (объемная геометрическая фигура), полученное вращением прямоугольного треугольника вокруг его катета как оси.
Определение. Шар — это тело (объемная геометрическая фигура), полученное вращением полукруга вокруг его диаметра как оси.
Развертки цилиндра и конусаРазверткой геометрической фигуры называется изображение плоскости, ограничивающей фигуру, в одной плоскости листа по размерам фигуры. Развертка цилиндра приведена схематически. Развертка конуса приведена схематически. Площади боковой поверхности цилиндра и конусаПравило. Площадь боковой поверхности цилиндра равна произведению длины окружности основания и высоты цилиндра. где C — длина окружности, H — высота цилиндра, R — радиус окружности основания. Правило. Площадь боковой поверхности конуса равна произведению половины длины окружности основания и образующей конуса. где C — длина окружности основания, l — длина образующей конуса, R — радиус основания. Площадь поверхности шараПравило. Площадь поверхности шара равна учетверенной площади большого круга шара. где R — радиус шара. Объемы цилиндра, конуса и шараПравило. Объем цилиндра равен произведению площади основания н высоты. где R — радиус основания, H — высота цилиндра. Правило. Объем конуса равен одной трети произведения площади основания и высоты конуса. где R — радиус основания, H — высота конуса. Правило. Объем шара равен четырем третямпроизведения числа Пи на куб радиуса.
где R — радиус шара. shkolo.ru Формулы объема, площади поверхности, объем конуса, объем цилиндра, объем шара
Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло. Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.
Ты нашел то, что искал? Поделись с друзьями! Смотрите также: Формулы объема и площади поверхности многогранников.Кроме формул, в решении задач по стереометрии нужны также элементарная логика и пространственное воображение. Есть и свои небольшие секреты. Например, такой важный факт: Если все линейные размеры объемного тела увеличить в 2 раза, то площадь его поверхности увеличится в 4 раза, а объем - в 8 раз. (ведь , ). Вот такая задача. Как и остальные на нашем сайте, она взята из банка заданий ФИПИ. 1. Объем конуса равен . Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. Для решения некоторых задач полезны начальные знания стереометрии. Например — что такое правильная пирамида или прямая призма. Полезно помнить, что у цилиндра, конуса и шара есть еще общее название — тела вращения. Что сферой называется поверхность шара. А, например, фраза «образующая конуса наклонена к плоскости основания под углом 30 градусов предполагает, что вы знаете, что такое угол между прямой и плоскостью. Вам также может пригодиться теорема Пифагора и простые формулы площадей фигур. Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу. 2. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду? Говорят, что хороший чертеж - это уже половина решения. Читайте о том, как строить чертежи в задачах по стереометрии. Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ». А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней. Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве) Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним. ege-study.ru Выкройка овального и наклонного конуса24.09.2014 // Владимир Трунов
Теперь речь пойдет о том, как построить выкройку (развертку) для овального и наклонного конуса. Под овальным конусом будем подразумевать конус, в основании которого лежит эллипс (как наиболее гармоничный из овалов). Наклонным конусом назовем конус, проекция вершины которого (или мнимой вершины, если конус усеченный) на плоскость основания не совпадает с центром эллипса.И тут я должен сообщить две новости, как водится, хорошую и плохую. Начну с плохой. Не существует простых формул для построения таких выкроек. Есть только жуткие интегралы. Но в них мы закапываться не будем благодаря хорошей новости: у нас есть компьютер. И есть такое понятие как численные методы. Коротко говоря, это выполнение огромного количества простейших операций над числами, в результате которых появляется возможность решить задачу, нерешаемую аналитически (то есть при помощи формул). И надо только найти человека, который изобрел бы алгоритм для решения нашей задачи, и хорошо ему заплатить. К счастью, такой человек нашелся, придумал алгоритм, запрограммировал его и публикует сегодня в виде новой версии программы Cones. Зовут его Владимир Трунов, и все благодарности — к нему. Нет никакого смысла вникать в подробности численного метода, реализованного в программе Cones для построения выкроек овальных и наклонных конусов. Скажу только, что основой его является разбиение эллипса на множество мелких отрезков и вычисление для каждой вершины полученного многоугольника значений длины образующей конуса и приращения угла развертки. Благодаря этому в вычислениях используются только тригонометрические функции и теорема Пифагора. Понятно, что полученные значения, а стало быть и рисунок, построенный по ним, имеют некоторую погрешность. Эта погрешность тем меньше, чем ближе конус к круглому и прямому. Если отношение большего диаметра эллипса к меньшему не превышает 2, а угол наклона оси (от вертикали) — не более 30 градусов, то погрешность в линейных размерах боковой поверхности выкройки не выйдет за 1%. (В более экзотических случаях погрешность может быть и больше, но в следующих версиях программы алгоритм будет совершенствоваться с целью ее минимизации.) tvlad.ru
gavrilovart.ru Конус как геометрическая фигураКонус (с греческого «konos») – сосновая шишка. Конус знаком людям с глубокой древности. В 1906 году была обнаружена книга «О методе», написанная Архимедом (287-212 гг. до н. э.), в этой книге дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед говорит, что это открытие принадлежит древнегреческому философу Демокриту (470-380 гг. до н.э.), который с помощью данного принципа получил формулы для вычисления объема пирамиды и конуса. Конус (круговой конус) – тело, которое состоит из круга – основание конуса, точки, не принадлежащей плоскости этого круга, – вершины конуса и всех отрезков, соединяющих вершину конуса и точки окружности основания. Отрезки, которые соединяют вершину конуса с точками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности. Конус называется прямым, если прямая, которая соединяет вершину конуса с центром основания, перпендикулярна плоскости основания. Прямой круговой конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси. Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого конуса называется прямая, содержащая его высоту. Сечение конуса плоскостью, проходящей через образующую конуса и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью конуса. Плоскость, перпендикулярная оси конуса, пересекает конус по кругу, а боковую поверхность – по окружности с центром на оси конуса. Плоскость, перпендикулярная оси конуса отсекает от него меньший конус. Оставшаяся часть называется усечённым конусом. Объём конуса равен трети произведения высоты на площадь основания. Таким образом, все конусы, опирающиеся на данное основание и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны. Площадь боковой поверхности конуса можно найти по формуле: Sбок = πRl, где R – радиус основания, l – длина образующей. Площадь полной поверхности конуса находится по формуле: Sкон = πRl + πR2, где R – радиус основания, l – длина образующей. Объём кругового конуса равен V = 1/3 πR2H, где R – радиус основания, Н – высота конуса Площадь боковой поверхности усеченного конуса можно найти по формуле: Sбок = π(R + r)l, где R – радиус нижнего основания, r – радиус верхнего основания, l – длина образующей. Площадь полной поверхности усеченного конуса можно найти по формуле: Sкон = πR2 + πr2 + π(R + r)l, где R – радиус нижнего основания, r – радиус верхнего основания, l – длина образующей. Объём усечённого конуса можно найти следующим образом: V = 1/3 πH(R2 + Rr + r2), где R – радиус нижнего основания, r – радиус верхнего основания, Н – высота конуса. © blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна. blog.tutoronline.ru Конус. Основание конуса. Конус основания высота. Объем конуса.Конус представляет собой трехмерный объект, несколько похожий по форме на пирамиду. На самом деле, вы можете представить себе конус как пирамиду, которая имеет бесконечное количество сторон (или, другими словами, пирамиду с круглым основанием). Однако конус не является многогранником, просто потому, что он имеет круглое основание. Она имеет одну вершину (вершину конуса), которая лежит на некотором расстоянии от основания и в другой плоскости. В то время как пирамида имеет конечное число треугольных сторон, каждая из которых соединяет одну сторону базового многоугольника с вершиной пирамиды, конус имеет единую, плавно изогнутую и коническую боковую поверхность, которая соединяет круглое основание конуса с его вершиной. На рисунке ниже показана квадратная пирамида и типичный конус с аналогичными пропорциями. На рисунке ниже, для прямого кругового конуса и наклонного кругового конуса, \(r\)-радиус основания, а \(h\)-высота конуса. На рисунке конуса слева \(s\)-наклонная высота конуса, то есть расстояние между вершиной конуса и периметром основания конуса.
փ-апертура конуса - это максимальный угол, который может существовать между двумя отрезками линии, соединяющими основание конуса с его вершиной.
Формула для нахождения объема кругового конуса (правого или смещенного) в значительной степени совпадает с формулой для нахождения объема пирамиды. Объем \(V\) будет произведением площади основания \(S_{осн}\) и вертикальной высоты конуса \(h\), умноженной на одну треть . Мы можем выразить это формально как: \(V =\frac{ 1}{3} S_{осн}h\) Обратите внимание, что это та же формула, которая используется для поиска объема пирамиды. Однако, поскольку основание конуса является окружностью, а площадь окружности вычисляется как \(\pi r^2\), где \(r\)-радиус окружности, то если мы подставим в формулу выше площадь окружности получим формулу объема конуса: \(V =\frac{ 1}{3} \pi r^2 h\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы "Альфа". Запишитесь на пробное занятие уже сейчас! Запишитесь на бесплатное тестирование знаний! myalfaschool.ru Как сделать развертку – выкройку для конуса или усеченного конуса заданных размеров. Простой расчет развертки.Иногда возникает задача – изготовить защитный зонт для вытяжной или печной трубы, вытяжной дефлектор для вентиляции и т.п. Но прежде чем приступить к изготовлению, надо сделать выкройку (или развертку) для материала. В интернете есть всякие программы для расчета таких разверток. Однако задача настолько просто решается, что вы быстрее рассчитаете ее с помощью калькулятора (в компьютере), чем будете искать, скачивать и разбираться с этими программами. Начнем с простого варианта — развертка простого конуса. Проще всего объяснить принцип расчета выкройки на примере.  Допустим, нам надо изготовить конус диаметром D см и высотой H сантиметров. Совершенно понятно, что в качестве заготовки будет выступать круг с вырезанным сегментом. Известны два параметра – диаметр и высота. По теореме Пифагора рассчитаем диаметр круга заготовки (не путайте с радиусом готового конуса). Половина диаметра (радиус) и высота образуют прямоугольный треугольник. Поэтому:  Итак, теперь мы знаем радиус заготовки и можем вырезать круг. Вычислим угол сектора, который надо вырезать из круга. Рассуждаем следующим образом: Диаметр заготовки равен 2R, значит, длина окружности равна Пи*2*R — т.е. 6.28*R. Обозначим ее L. Окружность полная, т.е. 360 градусов. А длина окружности готового конуса равна Пи*D. Обозначим ее Lm. Она, естественно, меньше чем длина окружности заготовки. Нам нужно вырезать сегмент с длиной дуги равной разности этих длин. Применим правило соотношения. Если 360 градусов дают нам полную окружность заготовки, то искомый угол должен дать длину окружности готового конуса.  Из формулы соотношения получаем размер угла X. А вырезаемый сектор находим путем вычитания 360 – Х. Из круглой заготовки с радиусом R надо вырезать сектор с углом (360-Х). Не забудьте оставить небольшую полоску материала для нахлеста (если крепление конуса будет внахлест). После соединения сторон вырезанного сектора получим конус заданного размера. Например: Нам нужен конус для зонта вытяжной трубы высотой (Н) 100 мм и диаметром (D) 250 мм. По формуле Пифагора получаем радиус заготовки – 160 мм. А длина окружности заготовки соответственно 160 x 6,28 = 1005 мм. В тоже время длина окружности нужного нам конуса — 250 x 3,14 = 785 мм. Тогда получаем, что соотношение углов будет такое: 785 / 1005 x 360 = 281 градус. Соответственно вырезать надо сектор 360 – 281 = 79 градусов. Расчет заготовки выкройки для усеченного конуса.Такая деталь бывает нужна при изготовлении переходников с одного диаметра на другой или для дефлекторов Вольперта-Григоровича или Ханженкова. Их применяют для улучшения тяги в печной трубе или трубе вентиляции. Задача немного осложняется тем, что нам неизвестна высота всего конуса, а только его усеченной части. Вообще же исходных цифр тут три: высота усеченного конуса Н, диаметр нижнего отверстия (основания) D, и диаметр верхнего отверстия Dm (в месте сечения полного конуса). Но мы прибегнем к тем же простым математическим построениям на основе теоремы Пифагора и подобия.  В самом деле, очевидно, что величина (D-Dm)/2 (половина разности диаметров) будет относиться с высотой усеченного конуса Н так же, как и радиус основания к высоте всего конуса, как если бы он не был усечен. Находим полную высоту (P) из этого соотношения. (D – Dm)/ 2H = D/2P Отсюда Р = D x H / (D-Dm).  Теперь зная общую высоту конуса, мы можем свести решение задачи к предыдущей. Рассчитать развертку заготовки как бы для полного конуса, а затем «вычесть» из нее развертку его верхней, ненужной нам части. А можем рассчитать непосредственно радиусы заготовки. Получим по теореме Пифагора больший радиус заготовки — Rz. Это квадратный корень из суммы квадратов высоты P и D/2. Меньший радиус Rm – это квадратный корень из суммы квадратов (P-H) и Dm/2. Теперь осталось рассчитать угол сектора, который надо вырезать. Длина окружности нашей заготовки равна 2 х Пи х Rz, или 6,28 х Rz. А длина окружности основания конуса – Пи х D, или 3,14 х D. Соотношение их длин и дадут соотношение углов секторов, если принять, что полный угол в заготовке – 360 градусов. Т.е. Х / 360 = 3,14 x D / 6.28 x Rz Отсюда Х = 180 x D / Rz (Это угол, который надо оставить, что бы получить длину окружности основания). А вырезать надо соответственно 360 – Х.  Например: Нам надо изготовить усеченный конус высотой 250 мм, диаметр основание 300 мм, диаметр верхнего отверстия 200 мм. Находим высоту полного конуса Р: 300 х 250 / (300 – 200) = 600 мм По т. Пифагора находим внешний радиус заготовки Rz: Корень квадратный из (300/2)^2 + 6002 = 618,5 мм По той же теореме находим меньший радиус Rm: Корень квадратный из (600 – 250)^2 + (200/2)^2 = 364 мм. Определяем угол сектора нашей заготовки: 180 х 300 / 618,5 = 87.3 градуса. На материале чертим дугу с радиусом 618,5 мм, затем из того же центра – дугу радиусом 364 мм. Угол дуги может имеет примерно 90-100 градусов раскрытия. Проводим радиусы с углом раскрытия 87.3 градуса. Наша заготовка готова. Не забудьте дать припуск на стыковку краев, если они соединяются внахлест. Константин Тимошенко © 31.07.2014 г. www.delaysam.ru |

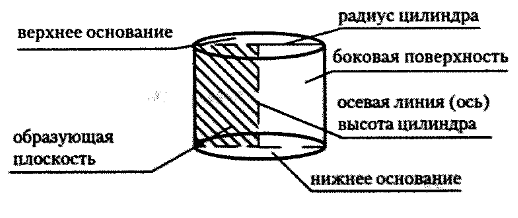
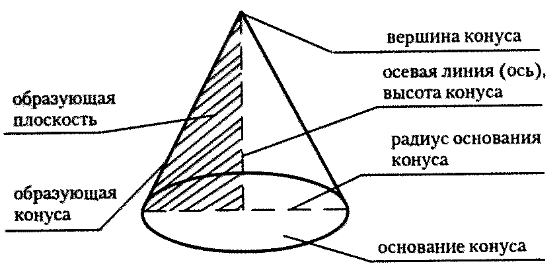


 Тела вращения, изучаемые в школе, - это цилиндр, конус и шар.
Тела вращения, изучаемые в школе, - это цилиндр, конус и шар.
 Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум.
Очевидно, что объем меньшего конуса в раз меньше объема большого и равен двум. Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в
Всё просто — рисуем вид снизу. Видим, что радиус большего круга в раз больше, чем радиус меньшего. Высоты у обоих конусов одинаковы. Следовательно, объем большего конуса будет в  В статье Выкройка для конуса мы рассмотрели построение выкройки для круглого прямого конуса, то есть конуса, имеющего в основании круг, и ось которого перпендикулярна основанию. Там мы обошлись несколькими простыми формулами.
В статье Выкройка для конуса мы рассмотрели построение выкройки для круглого прямого конуса, то есть конуса, имеющего в основании круг, и ось которого перпендикулярна основанию. Там мы обошлись несколькими простыми формулами.